一元二次方程实根分布
发布时间:2022-04-30 点击量:1425次
独立思考:
若函数f(x)为定义域D上的单调函数,且存在![]() (其中a<b),使得当x∊[a,b]时,f(x)的值域恰为
(其中a<b),使得当x∊[a,b]时,f(x)的值域恰为![]() ,则称函数f(x)是D上的正函数,[a,b]叫做“等域区间”
,则称函数f(x)是D上的正函数,[a,b]叫做“等域区间”
(1)已知![]() 是
是![]() 上的“正函数”,求
上的“正函数”,求![]() 的“等域区间”
的“等域区间”
(2)试探究是否存在实数m,使得函数![]() 是
是![]() 上的“正函数”?若存在,求出实数m的取值范围;若不存在,请说明理由
上的“正函数”?若存在,求出实数m的取值范围;若不存在,请说明理由
动态解析: 点击查看
教师讲解: 点击查看
(1)![]() 是
是![]() 上的“正函数”,且在
上的“正函数”,且在![]() 上单调递增
上单调递增
所以当![]() 时,
时,![]() 即
即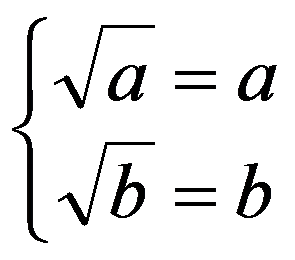
解得:![]()
故函数![]() 的“等域区间”为
的“等域区间”为![]()
(2)函数![]() 是
是![]() 上单调递减,
上单调递减,
因为g(x)是(-∞,0)上的“正函数”
所以当![]() 时,
时,![]() ,即
,即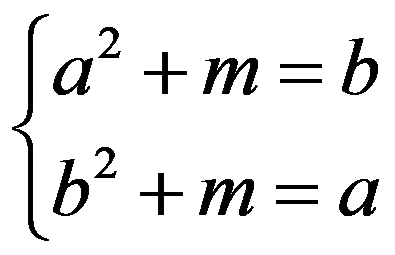
两式相减得:![]() 即
即![]()
代入![]() 得
得![]()
由![]() 且
且![]() 得
得![]()
故关于a的方程![]() 在区间
在区间![]() 内有实数解
内有实数解
令φ(a)= -a2-a-1=-(a+![]() )2-
)2-![]() ,则φ(a)在(-1,-
,则φ(a)在(-1,-![]() )的值域为(-1,-
)的值域为(-1,-![]() )
)
∴实数m的取值范围为(-1,-![]() )
)

