方程根的问题
发布时间：2022-04-28 点击量：1154次
独立思考:
设f(x)，g(x)是定义在R上的两个周期函数，f(x)的周期为4，g(x)的周期为2，且f(x)是奇函数，当x∊(0,2]时，f(x)＝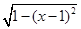
，g(x)＝
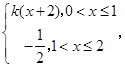其中k＞0。若在区间(0,9]上，关于x的方程f(x)＝g(x)有8个不同的实数根，则k的取值范围是 .
动态解析: 点击查看
教师讲解: 点击查看
作出函数f(x)与g(x)的图像
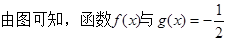(1＜x≤2，3＜x＜4，5＜x≤6，7＜x＜8)仅有2个交点；
要使关于x的方程f(x)＝g(x)有8个不同的实数根，
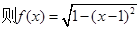，x∊(0,2]与g(x)＝k(x＋2)，x∊(0,1]的图像有2个不同交点，
由(1,0)到直线kx−y＋2k＝0的距离为1，得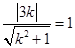
，
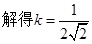(k＞0)，
因为两点(−2,0)，(1,1)连线的斜率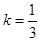
，
所以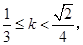
即k的取值范围为
